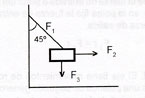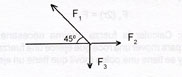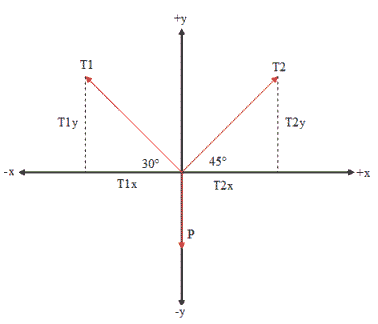
Esta condición de equilibrio implica que una fuerza aislada aplicada sobre un cuerpo no puede producir por sí sola equilibrio y que, en un cuerpo en equilibrio, cada fuerza es igual y opuesta a la resultante de todas las demás. Así, dos fuerzas iguales y opuestas, actuando sobre la misma línea de acción, sí producen equilibrio.
El equilibrio puede ser de tres clases: estable, inestable e indiferente. Si un cuerpo está suspendido, el equilibrio será estable si el centro de gravedad está por debajo del punto de suspensión; inestable si está por encima, e indiferente si coinciden ambos puntos. Si un cuerpo está apoyado, el equilibrio será estable cuando la vertical que pasa por el centro de gravedad caiga dentro de su base de sustentación; inestable cuando pase por el límite de dicha base, e indiferente cuando la base de sustentación sea tal que la vertical del centro de gravedad pase siempre por ella.